今回は、githubで「化合物が水にどれくらい溶けるか?」をまとめたデータセットを見つけたので、機械学習してみました。初心者向けの内容ですのでぜひコードを実践してみてください〜。
水溶解度を予測する意義
「この化合物は水にどのくらい溶けるか?」このような水への溶解度(log S)は、創薬や材料開発で欠かせない指標です。
log S とは?
溶解度 S(mol L−1)の常用対数を取った値 log S=log10(S)です。
たとえば、 S=10−3 mol L−1のとき log S=−3 となります。値が小さいほど水に溶けにくいことを意味し、実務上は –6 〜 +2 程度の範囲で議論されることが多いです。
溶解度が低いと、薬物として体内に吸収されにくかったり、実験操作が難しくなったりします。
もし構造式(SMILES)が分かるだけで、溶解度をコンピュータで素早く推定できたら、研究はぐっと効率化できますよね。本シリーズでは、オープンソースの RDKit と機械学習ライブラリ scikit-learn を活用し、Python で QSAR(Quantitative Structure–Activity/Property Relationship) モデルを組み立てる流れを解説します。
この記事でわかること
- SMILES を Python に読み込み、扱いやすい形に整える
- 分子構造を数値特徴量(記述子)へ変換する
- シンプルな回帰モデルで水溶解度を予測し、性能を評価する
プログラミングや機械学習が初めての化学・創薬系の研究者や学生の方でも取り組みやすい内容にしました。それでは始めていきましょう!
▼ 筆者のケモインフォマティクスおすすめ本
環境とデータセットを準備しよう
開発環境は以前私が記事で書いたDocker + VSCode (もしくはCursor)のデータサイエンス環境を使います。もう少し手軽に取り組みたい方は「Google Colaboratory」なども活用してみてください!
まずは必要なライブラリをインポートします。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from rdkit import Chem
from rdkit.Chem import Descriptors
from rdkit.Chem.PandasTools import AddMoleculeColumnToFrame
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
%matplotlib inline
sns.set_style('whitegrid')次に、今回の題材となるESOLデータセットを読み込みます。これは、1128個の化合物について、その構造(SMILES形式)と、実験で測定された水溶解度(logS)がまとめられた、この分野では非常に有名なデータセットです。
# データセットのURL
url = 'https://raw.githubusercontent.com/deepchem/deepchem/master/datasets/delaney-processed.csv'
# pandasでCSVファイルを読み込む
df = pd.read_csv(url)
# まずはデータの最初の5行を見てみる
df.head()df.head()の出力は以下の画像のようになります。
公開されているデータはすでに前処理されたデータなので、さまざまな特徴量を含んでいます。

実際には、前処理されていないデータは目的変数と化合物のsmilesのみを含むことが多いです。
ここでは、目的変数である「measured log solubility in mols per litre」と構造データである「smiles」の2つのカラムを使って、予測モデルを構築してみます。
# 目的変数とsmilesデータ以外を削除
cols_to_keep = ["measured log solubility in mols per litre", "smiles"]
df = df[cols_to_keep].copy()
# カラム名が長いため、簡潔な名前に変更
df = df.rename(columns={'measured log solubility in mols per litre': 'logS'})この処理を行うと、dfの中身は以下のようになります。
| logS | smiles | |
| 0 | -0.770 | OCC3OC(OCC2OC(OC(C#N)c1ccccc1)C(O)C(O)C2O)C(O)… |
|---|---|---|
| 1 | -3.300 | Cc1occc1C(=O)Nc2ccccc2 |
| 2 | -2.060 | CC(C)=CCCC(C)=CC(=O) |
| 3 | -7.870 | c1ccc2c(c1)ccc3c2ccc4c5ccccc5ccc43 |
| 4 | -1.330 | c1ccsc1 |
logSが予測したい対象ですので、smilesデータから特徴量を作成し、予測モデルを作っていきます。
SMILES を Mol オブジェクトへ変換する — RDKit の基本操作
SMILES 文字列は人間には便利ですが、計算機が分子構造を扱うには RDKit の Mol オブジェクト へ変換する必要があります。AddMoleculeColumnToFrame を使うと、DataFrame に Mol オブジェクト列を一括追加できるので非常に便利です。
# SMILES列からRDKitのMolオブジェクトを生成し、'ROMol'という新しい列を追加
AddMoleculeColumnToFrame(df, smilesCol='smiles', molCol='ROMol')
df.head()以下がdf.head()の出力です。ROMolというカラムが追加されました。(尺の都合上最初の2行だけ)
| logS | smiles | ROMol | |
|---|---|---|---|
| 0 | -0.77 | OCC3OC(OCC2OC(OC(C#N)c1ccccc1)C(O)C(O)C2O)C(O)… | <rdkit.Chem.rdchem.Mol object at 0xffff3d525af0> |
| 1 | -3.30 | Cc1occc1C(=O)Nc2ccccc2 | <rdkit.Chem.rdchem.Mol object at 0xffff3d524ac0> |
目的変数 log S の分布を可視化する
次に、今回予測したい 水溶解度(log S) がどのような分布を取っているか確認します。ターゲット変数の傾向を把握しておくと、モデル選択や前処理方針を決めるうえで役立ちます。
plt.figure(figsize=(8, 6))
sns.histplot(df["logS"], kde=True, bins=30)
plt.title("Distribution of Aqueous Solubility (logS)")
plt.xlabel("logS (measured)")
plt.ylabel("Frequency")
plt.show()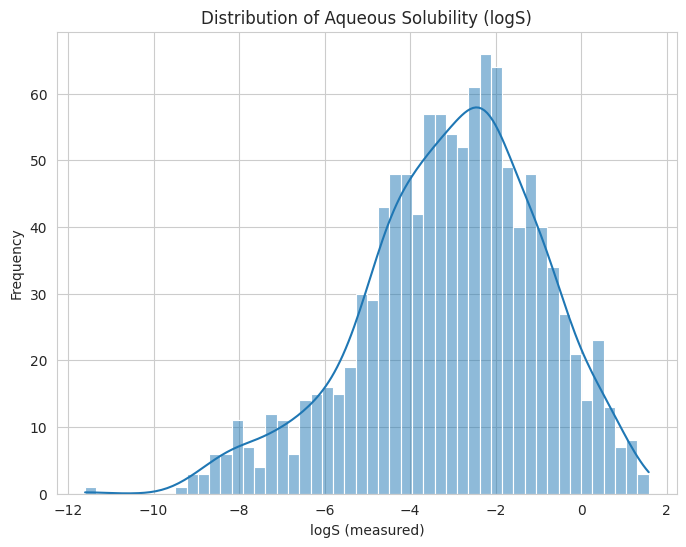
出力されたヒストグラムを見ると、多くの化合物のlogSが –5 〜 0 の範囲に集中し、概ね正規分布に近い形を示しています。この情報は後ほど回帰モデルを組む際の指標となります。
分子の特徴を数値化する ― 特徴量エンジニアリング
ここからが機械学習の本番です。モデルに水溶解度(log S)を予測させるには、「分子のどのような性質が溶解度に影響するか」を数値で表現し、入力データ(特徴量)として渡す必要があります。
ESOL の元論文(https://pubs.acs.org/doi/10.1021/ci034243x)では、以下の 4 つのベーシックな化学記述子(ケモインフォマティクスにおける特徴量)が用いられました。今回はこちらを試してみます。
| 記述子 | 意味 |
|---|---|
| MolLogP | 分子の疎水性(log P)。値が大きいほど油に溶けやすく、水に溶けにくい傾向があります。 |
| MolWt | 分子量。原子量の総和です。 |
| NumRotatableBonds | 自由回転できる単結合の本数。大きいほど分子が柔軟です。 |
| AromaticProportion | 分子中の原子のうち、芳香環に属する原子の割合。 |
RDKit を使って、これらの記述子を計算してみます。以下では、Mol オブジェクトから 4 つの記述子を算出し、特徴量の行列 X と目的変数 y を整えます。
# 4 つの記述子を計算する関数
def calculate_esol_descriptors(mol):
mw = Descriptors.MolWt(mol)
logp = Descriptors.MolLogP(mol)
rb = Descriptors.NumRotatableBonds(mol)
# Aromatic Proportion (AP)
aromatic_flags = [atom.GetIsAromatic() for atom in mol.GetAtoms()]
num_heavy_atoms = mol.GetNumHeavyAtoms()
ap = aromatic_flags.count(True) / num_heavy_atoms if num_heavy_atoms else 0
return [logp, mw, rb, ap]
# すべての分子について記述子を計算
X_desc = np.array(df["ROMol"].apply(calculate_esol_descriptors).tolist())
# 目的変数 logS
y = df["logS"].values
# DataFrame に変換
feature_names = ["MolLogP", "MolWt", "NumRotatableBonds", "AromaticProportion"]
X_desc_df = pd.DataFrame(X_desc, columns=feature_names)
X_desc_df.head()以下がX_desc_df.head()の出力です。
| MolLogP | MolWt | NumRotatableBonds | AromaticProportion | |
|---|---|---|---|---|
| 0 | -3.10802 | 457.432 | 7.0 | 0.187500 |
| 1 | 2.84032 | 201.225 | 2.0 | 0.733333 |
| 2 | 2.87800 | 152.237 | 4.0 | 0.000000 |
| 3 | 6.29940 | 278.354 | 0.0 | 1.000000 |
| 4 | 1.74810 | 84.143 | 0.0 | 1.000000 |
これで、説明変数 X(4 つの分子記述子)と目的変数 y(log S)のセットアップが完了しました。次のステップでは、このデータを使って回帰モデルを学習させ、溶解度を予測していきます。
まずは線形回帰モデルで試してみよう
準備が整ったところで、いよいよ機械学習モデルを構築します。最初に取り組むのは、もっともシンプルで解釈しやすい 線形回帰 です。
線形回帰は、中学校で学ぶ y=ax+b を多変量に拡張したもので、n次元の分子記述子と溶解度 log S の間を「超平面」で近似します。
データ分割の鉄則
モデルを公正に評価するために、データは必ず「訓練用(train)」と「テスト用(test)」に分けます。今回は 80 % を訓練、20 % をテストにしました。
# 80 % : 20 % に分割
X_train, X_test, y_train, y_test = train_test_split(
X_desc_df, y, test_size=0.2, random_state=42
)
# 線形回帰モデルをインスタンス化
lr_model = LinearRegression()
# 訓練データで学習
lr_model.fit(X_train, y_train)
# テストデータで予測
y_pred_lr = lr_model.predict(X_test)これで学習と予測が完了です。次はこの学習済みのモデルを使い予測精度を評価します。
モデルを評価する ― RMSE と R²
モデルの精度を確かめる指標として、今回は RMSE と R² スコア を用います。
| 指標 | 意味 | 良い値 |
|---|---|---|
| RMSE | Root Mean Squared Error:誤差の大きさを表す(小さいほど良い) | 0 に近いほど良い |
| R² | 決定係数:データのばらつきをどれだけ説明できたか | 1 に近いほど良い |
# 評価指標の計算
rmse_lr = np.sqrt(mean_squared_error(y_test, y_pred_lr))
r2_lr = r2_score(y_test, y_pred_lr)
print("--- モデル 1:線形回帰(記述子 4 種)---")
print(f"RMSE : {rmse_lr:.3f}")
print(f"R² : {r2_lr:.3f}")
# 実測値と予測値を散布図で比較
plt.figure(figsize=(6, 6))
plt.scatter(y_test, y_pred_lr, alpha=0.5)
plt.plot([-8, 2], [-8, 2], "r--") # y = x
plt.title("Actual vs. Predicted (Linear Regression)")
plt.xlabel("Actual log S")
plt.ylabel("Predicted log S")
plt.axis("square")
plt.show()
# 出力
# -- モデル 1:線形回帰(記述子 4 種)---
# RMSE : 1.113
# R² : 0.738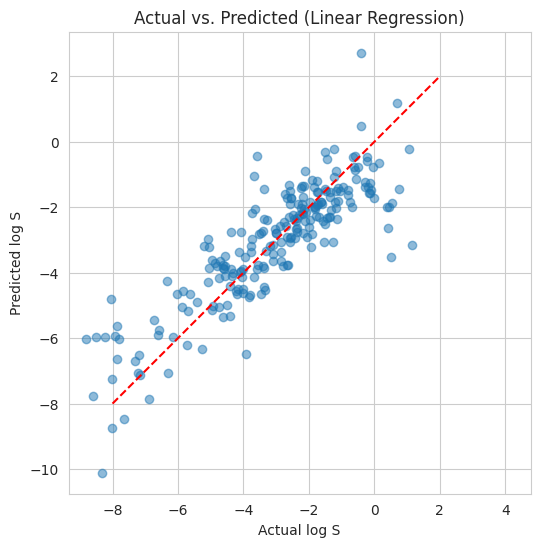
横軸が実測値、縦軸が線形回帰で予測された値となっています。
R² ≒ 0.74 という結果は、
「水溶解度のばらつきの約 74 % を、このモデルが説明できた」
ことを示しています。わずか 4 つの基本記述子だけで達成できたのは上々の滑り出しです。
特徴量の寄与を確認しよう
線形回帰の利点は、係数(重み) を通じて各特徴量の寄与を直接解釈できる点です。
print("\n--- 特徴量の係数 ---")
for name, coef in zip(feature_names, lr_model.coef_):
print(f"{name}: {coef:+.3f}")
# 出力
--- 特徴量の係数 ---
MolLogP : -0.755
MolWt : -0.006
NumRotatableBonds : -0.009
AromaticProportion : -0.352MolLogP (–0.755)
ログ P が大きい(疎水性が高い)ほど log S が大きく減少したことを意味しています。
つまり「油っぽいほど水に溶けにくい」という直感的な傾向をモデルが学習できています。
AromaticProportion (–0.352)
芳香環の割合が高いほど溶解度が低下していると解釈できます。こちらも化学的に納得できる傾向です。
まとめと次回予告
今回やったこと
- RDKit と pandas で化学データを読み込み、Mol オブジェクトを作成
- 分子記述子 4 種(MolLogP, MolWt, NumRotatableBonds, AromaticProportion)を計算
- 線形回帰モデル を学習し、テストデータで R² ≒ 0.74 を達成
- 係数を通して、モデルが化学的に妥当な関係を捉えていることを確認
RDKitを使った機械学習の例は意外とネット上のデータでも練習できますね。今後も記事を書いていくのでぜひチェックしてみてください。
次回は特徴量を増やしてみて、精度がどのように変化するかをみていきたいと思います。
以上です。ありがとうございました!
Noteで化学系就活のことや、研究生活のことなど書いているので覗いてもらえるとうれしいです!

続編です!↓




コメント