前回の記事では、4つの基本的な化学的特徴量(MolLogP, MolWtなど)を使って、化合物の水溶解度(logS)を予測する線形回帰モデルを構築しました。結果として、R²スコアが約0.74となり、最初のモデルとしては上出来な結果を得ることができました。
今回はRDKitで作成できる特徴量をもう少し増やしてみて、精度が上がるかを検証する特徴量エンジニアリングを実践してみます。
今回の特徴量エンジニアリングでは、前回使った4つの特徴量だけでは捉えきれなかった分子の性質を、化学の知識(ドメイン知識)を使って補うため、新たな特徴量を追加し、精度を向上させてみます。
▼ 筆者のケモインフォマティクスおすすめ本
実践1:極性・水素結合に関する特徴量を追加しよう!
水に溶けるかどうかを考える上で、分子の「極性(水との親和性)」が重要だと考えられます。
そこで、今回は以下の3つの極性に関する特徴量を追加してみましょう。全てRDKitを使って簡単に生成することができます。
| 特徴量 (RDKitで生成できる記述子) | 説明 |
| TPSA | トポロジカル分極性表面積。分子の表面のうち、極性を持つ原子(NやO)が占める面積であり、極性の高さを表す指標。 |
| NumHDonors | 水素結合ドナー数。強く正に分極する傾向のある水素有する部位(-OH, -NH₂など)の数。 |
| NumHAcceptors | 水素結合アクセプター数。強く負に分極する傾向のある部位(C=Oなど)の数。 |
前回作成した関数部分に少し修正を加えます。以下がコード全体と出力です。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from rdkit.Chem import Descriptors
from rdkit.Chem.PandasTools import AddMoleculeColumnToFrame
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
%matplotlib inline
sns.set_style('whitegrid')
# データセットのURL
url = 'https://raw.githubusercontent.com/deepchem/deepchem/master/datasets/delaney-processed.csv'
df = pd.read_csv(url)
# 目的変数とsmilesデータ以外を削除
cols_to_keep = ["measured log solubility in mols per litre", "smiles"]
df = df[cols_to_keep].copy()
# カラム名が長いため、簡潔な名前に変更
df = df.rename(columns={'measured log solubility in mols per litre': 'logS'})
AddMoleculeColumnToFrame(df, smilesCol='smiles', molCol='ROMol')
def calculate_all_descriptors(mol):
# --- 前回の記事の特徴量 ---
mw = Descriptors.MolWt(mol)
logp = Descriptors.MolLogP(mol)
rb = Descriptors.NumRotatableBonds(mol)
aromatic_flags = [atom.GetIsAromatic() for atom in mol.GetAtoms()]
num_heavy_atoms = mol.GetNumHeavyAtoms()
ap = aromatic_flags.count(True) / num_heavy_atoms if num_heavy_atoms else 0
# --- 新しい特徴量 ---
tpsa = Descriptors.TPSA(mol)
h_donors = Descriptors.NumHDonors(mol)
h_acceptors = Descriptors.NumHAcceptors(mol)
return [logp, mw, rb, ap, tpsa, h_donors, h_acceptors]
# 新しい特徴量リスト
new_feature_names = [
"MolLogP", "MolWt", "NumRotatableBonds", "AromaticProportion",
"TPSA", "NumHDonors", "NumHAcceptors"
]
# すべての分子について記述子を計算
X_desc = np.array(df["ROMol"].apply(calculate_all_descriptors).tolist())
# 目的変数 logS
y = df["logS"].values
X_desc_df = pd.DataFrame(X_desc, columns=new_feature_names)
X_desc_df.head()
X_train, X_test, y_train, y_test = train_test_split(
X_desc_df, y, test_size=0.2, random_state=42
)
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
y_pred_lr = lr_model.predict(X_test)
rmse_lr = np.sqrt(mean_squared_error(y_test, y_pred_lr))
r2_lr = r2_score(y_test, y_pred_lr)
# 実測値と予測値を散布図で比較
plt.figure(figsize=(6, 6))
plt.scatter(y_test, y_pred_lr, alpha=0.5)
plt.plot([-8, 2], [-8, 2], "r--") # y = x
plt.title("Actual vs. Predicted (Linear Regression)")
plt.xlabel("Actual log S")
plt.ylabel("Predicted log S")
plt.axis("square")
plt.show()
print("--- モデル精度---")
print(f"RMSE : {rmse_lr:.3f}")
print(f"R² : {r2_lr:.3f}")
print("\n--- 特徴量の係数 ---")
for name, coef in zip(new_feature_names, lr_model.coef_):
print(f"{name}: {coef:+.3f}")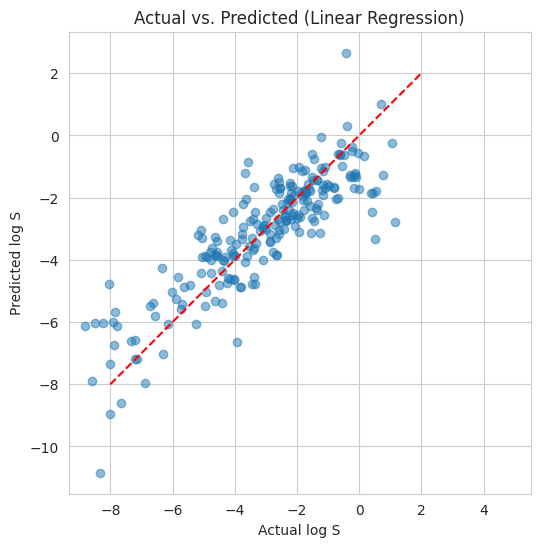
出力結果
--- モデル精度---
RMSE : 1.096
R² : 0.746
--- 特徴量の係数 ---
MolLogP: -0.865
MolWt: -0.005
NumRotatableBonds: -0.020
AromaticProportion: -0.309
TPSA: -0.014
NumHDonors: -0.066
NumHAcceptors: +0.181R²スコアが0.746に向上しました!(前回の4特徴量モデルは約0.74でした)。 3つの特徴量を加えただけで、モデルの精度が改善されています。
実践2:さらに特徴量を追加してみる
さらに特徴量を追加してみましょう。次は、分子の「形状」や「複雑さ」に関連する特徴量です。
| 特徴量 | 説明 |
| NumRings | 環の数。分子内に含まれる環状構造の総数。 |
| NumHeteroatoms | ヘテロ原子の数。炭素と水素以外の原子(O, N, Sなど)の数。 |
これらを追加するには先ほどのコードのcalculate_all_descriptors関数とnew_feature_namesのリストを以下のように書き換えます。
def calculate_all_descriptors(mol):
# --- 元の特徴量 ---
mw = Descriptors.MolWt(mol)
logp = Descriptors.MolLogP(mol)
rb = Descriptors.NumRotatableBonds(mol)
aromatic_flags = [atom.GetIsAromatic() for atom in mol.GetAtoms()]
num_heavy_atoms = mol.GetNumHeavyAtoms()
ap = aromatic_flags.count(True) / num_heavy_atoms if num_heavy_atoms else 0
# --- 新しい特徴量 ---
tpsa = Descriptors.TPSA(mol)
h_donors = Descriptors.NumHDonors(mol)
h_acceptors = Descriptors.NumHAcceptors(mol)
num_rings = Descriptors.RingCount(mol)
num_hetero = Descriptors.NumHeteroatoms(mol)
return [logp, mw, rb, ap, tpsa, h_donors, h_acceptors, num_rings, num_hetero]
# 新しい特徴量の名前リストも更新する
new_feature_names = [
"MolLogP", "MolWt", "NumRotatableBonds", "AromaticProportion",
"TPSA", "NumHDonors", "NumHAcceptors", "NumRings", "NumHeteroatoms"
]出力結果
--- モデル精度---
RMSE : 1.077
R² : 0.755
--- 特徴量の係数 ---
MolLogP: -0.819
MolWt: -0.000
NumRotatableBonds: -0.117
AromaticProportion: -0.092
TPSA: -0.008
NumHDonors: -0.088
NumHAcceptors: +0.257
NumRings: -0.379
NumHeteroatoms: -0.142先ほどよりもR²スコアが0.755と高くなっています。 3つの特徴量を加えただけで、モデルの精度が改善されています。
一方で、モデルの係数を見てみると、NumHDonorsの相関は高くなく、化学的な解釈からは違和感があります。これはおそらく、多重共線性という現象で、「モデルに入力する特徴量同士が、互いに似すぎている状態」であることが示唆されます。
ここら辺は次回の記事で多重共線性の解消のための「特徴量選択」に関する手法を紹介できればと思います。
まとめ
今回は、予測精度を向上させるための「特徴量エンジニアリング」をやってみました。
化学の知識に基づいて予測に役立ちそうな新しい特徴量を追加することで、極性や水素結合に関する特徴量(TPSAなど)が、モデルの性能向上に貢献することを確認できました。
次回以降は「多重共線性の解消」や「ランダムフォレスト」に取り組んでみようと思います。
続編です!↓




コメント