Python(RDKit)で学ぶ特徴量選択：多重共線性を解消し、信頼できる物性予測モデルを構築する

2025.06.22
スポンサーリンク

前回の記事では、「特徴量エンジニアリング」によって新しい特徴量を追加し、モデルの予測精度（R²スコア）を向上させることに成功しました。

一方で、モデルの係数を見てみると、NumHDonorsの相関は高くないなど、化学的な解釈からは違和感がありました。これは多重共線性という現象で、「モデルに入力する特徴量同士が、互いに似すぎている状態」であることが示唆されます。

例えば、事件の目撃者が２人いたとして、それぞれが「犯人の身長は180 cm近くあった」、「犯人は身長がとても高かった」と話していれば、定量性の違いはあれど同じことを意味しています。多重共線性もこれに似たようなことが生じていると考えていいでしょう。

今回は、多重共線性の解消のための「特徴量選択」に関する手法を紹介できればと思います。

回避策①：相関行列で似た特徴量のペアを見つける

最も直感的で分かりやすい方法が、特徴量同士の相関関係を直接確認することです。

相関行列の計算と可視化

まずは、前回作成した9つの特徴量を持つデータフレーム (X_desc_df) を使って、特徴量同士の相関係数を計算し、ヒートマップで可視化してみましょう。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from rdkit.Chem import Descriptors
from rdkit.Chem.PandasTools import AddMoleculeColumnToFrame
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

%matplotlib inline
sns.set_style('whitegrid')


# データセットのURL
url = 'https://raw.githubusercontent.com/deepchem/deepchem/master/datasets/delaney-processed.csv'

# pandasでCSVファイルを読み込む
df = pd.read_csv(url)

# 目的変数とsmilesデータ以外を削除
cols_to_keep = ["measured log solubility in mols per litre", "smiles"]
df = df[cols_to_keep].copy() 
# カラム名が長いため、簡潔な名前に変更
df = df.rename(columns={'measured log solubility in mols per litre': 'logS'})

# SMILES列からRDKitのMolオブジェクトを生成し、'ROMol'という新しい列を追加
AddMoleculeColumnToFrame(df, smilesCol='smiles', molCol='ROMol')


def calculate_all_descriptors(mol):
    mw   = Descriptors.MolWt(mol)
    logp = Descriptors.MolLogP(mol)
    rb   = Descriptors.NumRotatableBonds(mol)
    aromatic_flags   = [atom.GetIsAromatic() for atom in mol.GetAtoms()]
    num_heavy_atoms  = mol.GetNumHeavyAtoms()
    ap = aromatic_flags.count(True) / num_heavy_atoms if num_heavy_atoms else 0
    tpsa = Descriptors.TPSA(mol)
    h_donors = Descriptors.NumHDonors(mol)
    h_acceptors = Descriptors.NumHAcceptors(mol)
    num_rings = Descriptors.RingCount(mol)
    num_hetero = Descriptors.NumHeteroatoms(mol)
    
    return [logp, mw, rb, ap, tpsa, h_donors, h_acceptors, num_rings, num_hetero]

new_feature_names = [
    "MolLogP", "MolWt", "NumRotatableBonds", "AromaticProportion",
    "TPSA", "NumHDonors", "NumHAcceptors", "NumRings", "NumHeteroatoms"
]

X_desc = np.array(df["ROMol"].apply(calculate_all_descriptors).tolist())

y = df["logS"].values
X_desc_df = pd.DataFrame(X_desc, columns=new_feature_names)


# 特徴量同士の相関行列を計算
correlation_matrix = X_desc_df.corr()

# ヒートマップで可視化
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt='.2f')
plt.title('Feature Correlation Matrix')
plt.show()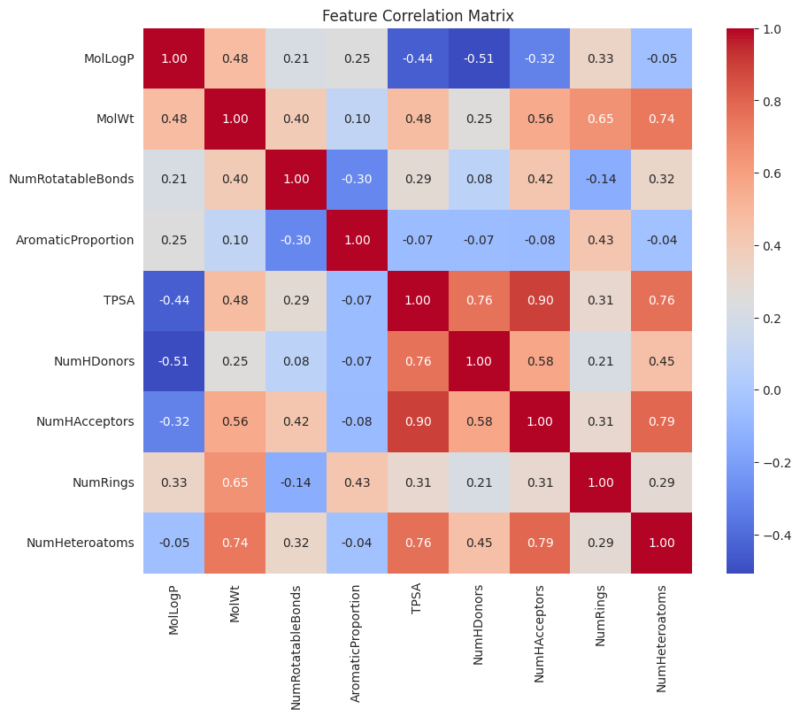

このヒートマップの見方は簡単です。

  • 色が赤に近いほど「正の相関」が強い（片方が増えると、もう片方も増える傾向）
  • 色が青に近いほど「負の相関」が強い（片方が増えると、もう片方は減る傾向）
  • 色の濃さが「似ている度合い」の指標になります。

似た特徴量の特定と対処

赤色のエリア

まず、右下の赤色が非常に濃いエリアに注目してください。

  • TPSA と NumHAcceptors の相関: 0.90
  • TPSA と NumHDonors の相関: 0.76
  • TPSA と NumHeteroatoms の相関: 0.76

これは、これらの特徴量が極めて強い正の相関、つまり「非常に似たような情報」を持っていることを示しています。これは化学的な観点から見ても自然なことです。

  • TPSAは、極性原子（主に酸素Oや窒素N）の表面積の合計です。
  • NumHAcceptorsは、水素結合アクセプター（主に酸素Oや窒素N）の数を数えたものです。
  • NumHDonorsは、水素結合ドナー（-OHや-NHのH）の数を数えたものです。
  • NumHeteroatomsはヘテロ原子の数を数えたものです。

つまり、この4つの特徴量は、呼び方が違うだけで、ほぼ同じ構造的な特徴を記述するものです。

青色のエリア

次に、青色が濃いエリアに注目してみましょう。

  • MolLogP と NumHDonors の相関: -0.51
  • MolLogP と TPSA の相関: -0.44

これは、これらがはっきりとした負の相関にあることを示しています。

この関係も、化学の基本原則そのものです。

  • MolLogPは「油っぽさ（脂溶性）」の指標です。
  • TPSA, NumHDonorsは「極性」の指標です。つまり水との親和性に近い特徴量でもあります。

つまり、「油っぽい分子ほど、水っぽい性質は低い」という、「水と油」の関係を示しています。

対処法1: 化学的な意味合い・包括性で選ぶ

このように特徴量同士の相関が強い場合は、相関の高いペアから代表的な特徴量を1つだけ選び、もう片方はモデルから除外します。 例えば、TPSA, NumHAcceptors, NumHDonors, NumHeteroatomsの中では、TPSAが最も総合的な極性の指標と考えられるため、TPSAを残して他の3つを削除する、といった判断が考えられます。

一方、負の相関を示す特徴量同士への対処法は「何もしない」が正解です。強い負の相関は、多重共線性の問題にはならず、 それどころか、モデルにとっては非常に有益な情報です。したがって、MolLogPについてはそのまま残します。

前回のコードから、TPSA, NumHAcceptors, NumHDonors, NumHeteroatomsのうち、TPSAを残して精度を見てみます。コードは以下のようになります。

import pandas as pd
import numpy as np
from rdkit import Chem
from rdkit.Chem import Descriptors
from rdkit.Chem.PandasTools import AddMoleculeColumnToFrame
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

url = 'https://raw.githubusercontent.com/deepchem/deepchem/master/datasets/delaney-processed.csv'
df = pd.read_csv(url)
cols_to_keep = ["measured log solubility in mols per litre", "smiles"]
df = df[cols_to_keep].copy() 
df = df.rename(columns={'measured log solubility in mols per litre': 'logS'})
AddMoleculeColumnToFrame(df, smilesCol='smiles', molCol='ROMol')

# 9つの特徴量をすべて計算する関数
def calculate_all_descriptors(mol):
    mw   = Descriptors.MolWt(mol)
    logp = Descriptors.MolLogP(mol)
    rb   = Descriptors.NumRotatableBonds(mol)
    aromatic_flags   = [atom.GetIsAromatic() for atom in mol.GetAtoms()]
    num_heavy_atoms  = mol.GetNumHeavyAtoms()
    ap = aromatic_flags.count(True) / num_heavy_atoms if num_heavy_atoms else 0
    tpsa = Descriptors.TPSA(mol)
    h_donors = Descriptors.NumHDonors(mol)
    h_acceptors = Descriptors.NumHAcceptors(mol)
    num_rings = Descriptors.RingCount(mol)
    num_hetero = Descriptors.NumHeteroatoms(mol)
    
    return [logp, mw, rb, ap, tpsa, h_donors, h_acceptors, num_rings, num_hetero]

# 特徴量のリスト
all_feature_names = [
    "MolLogP", "MolWt", "NumRotatableBonds", "AromaticProportion",
    "TPSA", "NumHDonors", "NumHAcceptors", "NumRings", "NumHeteroatoms"
]

# 全特徴量と目的変数を計算し、欠損値のある行を削除
X_all_list = df["ROMol"].apply(calculate_all_descriptors).tolist()
X_all_df = pd.DataFrame(X_all_list, columns=all_feature_names)
X_all_df['logS'] = df['logS']

y = X_all_df['logS'].values
X_all_df = X_all_df.drop('logS', axis=1)

# 'TPSA' を残し、相関の強い 'NumHDonors', 'NumHAcceptors', 'NumHeteroatoms' を除外
features_strategy1 = [
    "MolLogP", "MolWt", "NumRotatableBonds", "AromaticProportion",
    "TPSA", "NumRings"
]
X_strategy1_df = X_all_df[features_strategy1]

X_train1, X_test1, y_train1, y_test1 = train_test_split(X_strategy1_df, y, test_size=0.2, random_state=42)
model1 = LinearRegression().fit(X_train1, y_train1)
y_pred1 = model1.predict(X_test1)
rmse1 = np.sqrt(mean_squared_error(y_test1, y_pred1))
r2_1 = r2_score(y_test1, y_pred1)

print(f"選択した特徴量: {features_strategy1}")
print(f"RMSE: {rmse1:.4f}")
print(f"R² (決定係数): {r2_1:.4f}")
# 出力
選択した特徴量: ['MolLogP', 'MolWt', 'NumRotatableBonds', 'AromaticProportion', 'TPSA', 'NumRings']
RMSE: 1.0885
R² (決定係数): 0.7494

精度はR² (決定係数): 0.7494と全ての特徴量を選択した時（前回の0.755）と比べて若干の低下を示しました。

対処法2: 目的変数との相関の強さで選択する

「最終的に予測したいlogSと、より強く関係しているのはどちらか？」で判断します。予測精度を最優先するため、非常に実践的なアプローチですが、解釈性や汎用性の面では「対処法1」に劣る可能性もあります。

print("\n--- 戦略2：目的変数との相関の強さで選択 ---")

# 相関の高いグループとlogSの相関を計算
correlated_group = ["TPSA", "NumHDonors", "NumHAcceptors", "NumHeteroatoms"]
temp_df = X_all_df[correlated_group].copy()
temp_df['logS'] = y
logS_correlations = temp_df.corr()['logS'].abs().drop('logS')
best_feature = logS_correlations.idxmax()

print(f"相関の高いグループ: {correlated_group}")
print("各特徴量と logS との相関係数（絶対値）:")
print(logS_correlations)
print(f"\nlogSと最も相関が強い特徴量: '{best_feature}'")

# 'best_feature' を残し、相関グループの他の特徴量を除外
base_features = ["MolLogP", "MolWt", "NumRotatableBonds", "AromaticProportion", "NumRings"]
features_strategy2 = base_features + [best_feature]
features_strategy2 = list(dict.fromkeys(features_strategy2)) 
X_strategy2_df = X_all_df[features_strategy2]

X_train2, X_test2, y_train2, y_test2 = train_test_split(X_strategy2_df, y, test_size=0.2, random_state=42)
model2 = LinearRegression().fit(X_train2, y_train2)
y_pred2 = model2.predict(X_test2)
rmse2 = np.sqrt(mean_squared_error(y_test2, y_pred2))
r2_2 = r2_score(y_test2, y_pred2)

print(f"\n選択した特徴量: {features_strategy2}")
print(f"RMSE: {rmse2:.4f}")
print(f"R² (決定係数): {r2_2:.4f}")
# 出力
--- 戦略2：目的変数との相関の強さで選択 ---
相関の高いグループ: ['TPSA', 'NumHDonors', 'NumHAcceptors', 'NumHeteroatoms']
各特徴量と logS との相関係数（絶対値）:
TPSA              0.123210
NumHDonors        0.209429
NumHAcceptors     0.055728
NumHeteroatoms    0.184330
Name: logS, dtype: float64

logSと最も相関が強い特徴量: 'NumHDonors'

選択した特徴量: ['MolLogP', 'MolWt', 'NumRotatableBonds', 'AromaticProportion', 'NumRings', 'NumHDonors']
RMSE: 1.0676
R² (決定係数): 0.7589

最もlogSと相関が高かったのは、NumHDonorsであり、極性を示す4つの特徴量からこのNumHDonorsだけを選択した場合には、R² (決定係数): 0.7589と9個の全ての特徴量を選んだ時よりも精度が向上しています。

似た特徴量のペアから取捨選択するアプローチ：対処法1と2どちらが良いか？

一般的には、以下のようなことが言えます。精度をとるか、汎用性をとるか、の違いと言えます。

  • 化学的な意味合いで選ぶ（戦略1）は、モデルの解釈性や汎用性を高める上で優れたアプローチです。
  • 目的変数との相関で選ぶ（戦略2）は、とにかく予測精度を1%でも高めたい場合に有効なアプローチです。

回避策②：VIFで依存度を厳密にチェックする

相関行列は2つの特徴量間の関係しか見れませんが、VIF (Variance Inflation Factor; 分散拡大係数) を使えば、「ある1つの特徴量が、他の”すべて”の特徴量によって、どれだけ説明できてしまうか」を数値で評価できます。

VIFは独立変数間の多重共線性を検出するための指標の1つです。
言い換えるなら、その特徴量の”独自性のなさ”を測るスコアです。

  • VIFが高い: その特徴量は独自の情報が少なく、他の特徴量に依存している（＝重複度が高い）
  • VIFが低い: その特徴量は、他にはないユニークな情報を持っている

経験則として、VIFが10以上の場合、多重共線性が高いと判断し、その特徴量を分析から除くのが良いとされています。（ただし、5 以上でも注意が必要との文献もあります。）

VIFの計算と評価の実践

では、実際に私たちが使っている9つの特徴量について、VIFを計算してみましょう。VIFの計算にはstatsmodelsというライブラリが便利です。
詳しい理論は省略しますが、以下のようにしてVIFを計算できます。

# statsmodelsライブラリのインポート
# ※もし未インストールなら、お使いの環境で !pip install statsmodels を実行してください
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant

# X_all_dfは9つの特徴量すべてを含むDataFrame
X_const = add_constant(X_all_df) 

# 各特徴量のVIFを計算して、見やすいようにDataFrameに格納
vif_df = pd.DataFrame()
vif_df["feature"] = X_const.columns
vif_df["VIF"] = [variance_inflation_factor(X_const.values, i) for i in range(X_const.shape[1])]

print(vif_df[vif_df["feature"] != 'const'])
#　出力
              feature        VIF
1             MolLogP   8.876377
2               MolWt  15.986351
3   NumRotatableBonds   3.596596
4  AromaticProportion   1.547902
5                TPSA  12.187242
6          NumHDonors   3.355138
7       NumHAcceptors   9.320971
8            NumRings   5.965526
9      NumHeteroatoms   9.471839

重複度の高い特徴量 (VIF > 10):

  • MolWt (分子量) が 15.98
  • TPSA (極性表面積) が 12.18

この2つは、他の特徴量によってその情報の多くが説明できてしまう、最も重複度の高い特徴量であることが判明しました。

相関行列の分析ではTPSAと極性関連の特徴量の関係が強く疑われましたが、VIFで見てみると、MolWt（分子のサイズ）も他の多くの特徴量（NumRings, NumHeteroatomsなど）と強く関連しあっていることが数値で明らかになりました。

VIFに基づいて特徴量を選択する

VIFを使うときの重要な注意点として、「VIFが高いものを一度に全部削除しない」ということがあります。

なぜなら、ある特徴量を1つ削除すると、残された特徴量たちの関係性が変わり、VIFの値全体が変動するからです。そのため、正しい手順は、以下の反復プロセスです。

【一度目の反復操作】 最もVIFが高い特徴量を削除する

  1. 現在のVIFスコアを見ると、最も高いのは MolWt (VIF ≈ 16.0) です。
  2. まずはこのMolWtを、特徴量のリストから削除します。
X_df_round1 = X_all_df.drop('MolWt', axis=1)
X_const = add_constant(X_df_round1) 
vif_df = pd.DataFrame()
vif_df["feature"] = X_const.columns
vif_df["VIF"] = [variance_inflation_factor(X_const.values, i) for i in range(X_const.shape[1])]
print(vif_df[vif_df["feature"] != 'const'])
# 出力
              feature        VIF
1             MolLogP   5.880954
2   NumRotatableBonds   3.299089
3  AromaticProportion   1.389511
4                TPSA  12.031850
5          NumHDonors   2.934778
6       NumHAcceptors   9.237974
7            NumRings   3.603829
8      NumHeteroatoms   4.733952

VIFスコアの変化を観察する

この結果から、以下のことが分かります。

  1. MolWtとの関連が強かった特徴量のVIFが低下: MolWtを削除したことで、それと関連の強かったNumHeteroatoms（ヘテロ原子数）のVIFは9.47から4.73へと大きく下がり、問題のないレベルになりました。
  2. 次にVIFの高い特徴量: しかし、依然としてTPSAのVIFが12.03と非常に高いことがわかります。

したがって、次はTPSAを削除します。

# MolWtを削除済みのデータフレームから、さらに 'TPSA' を削除
X_df_round2 = X_df_round1.drop('TPSA', axis=1)

# VIFを再々計算する
X_const_round2 = add_constant(X_df_round2)
vif_df_round2 = pd.DataFrame()
vif_df_round2["feature"] = X_const_round2.columns
vif_df_round2["VIF"] = [variance_inflation_factor(X_const_round2.values, i) for i in range(X_const_round2.shape[1])]

print("--- TPSAを削除後のVIFスコア ---")
print(vif_df_round2[vif_df_round2["feature"] != 'const'])
# 出力
--- TPSAを削除後のVIFスコア ---
              feature       VIF
1             MolLogP  4.849478
2   NumRotatableBonds  3.105724
3  AromaticProportion  1.387803
4          NumHDonors  2.242873
5       NumHAcceptors  7.847526
6            NumRings  3.194219
7      NumHeteroatoms  3.835467

この結果から、VIFスコアはすべて10を下回っており、特にNumHAcceptorsが7.85と最も高いものの、許容範囲内と言えるでしょう。

この特徴量で精度を評価してみましょう。

import pandas as pd
import numpy as np
from rdkit import Chem
from rdkit.Chem import Descriptors
from rdkit.Chem.PandasTools import AddMoleculeColumnToFrame
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
import seaborn as sns

url = 'https://raw.githubusercontent.com/deepchem/deepchem/master/datasets/delaney-processed.csv'
df = pd.read_csv(url)
cols_to_keep = ["measured log solubility in mols per litre", "smiles"]
df = df[cols_to_keep].copy() 
df = df.rename(columns={'measured log solubility in mols per litre': 'logS'})
AddMoleculeColumnToFrame(df, smilesCol='smiles', molCol='ROMol')

# 9つの特徴量をすべて計算する関数
def calculate_all_descriptors(mol):
    mw   = Descriptors.MolWt(mol)
    logp = Descriptors.MolLogP(mol)
    rb   = Descriptors.NumRotatableBonds(mol)
    aromatic_flags   = [atom.GetIsAromatic() for atom in mol.GetAtoms()]
    num_heavy_atoms  = mol.GetNumHeavyAtoms()
    ap = aromatic_flags.count(True) / num_heavy_atoms if num_heavy_atoms else 0
    tpsa = Descriptors.TPSA(mol)
    h_donors = Descriptors.NumHDonors(mol)
    h_acceptors = Descriptors.NumHAcceptors(mol)
    num_rings = Descriptors.RingCount(mol)
    num_hetero = Descriptors.NumHeteroatoms(mol)
    
    return [logp, mw, rb, ap, tpsa, h_donors, h_acceptors, num_rings, num_hetero]

# 特徴量のリスト
all_feature_names = [
    "MolLogP", "MolWt", "NumRotatableBonds", "AromaticProportion",
    "TPSA", "NumHDonors", "NumHAcceptors", "NumRings", "NumHeteroatoms"
]

X_all_list = df["ROMol"].apply(calculate_all_descriptors).tolist()
X_all_df = pd.DataFrame(X_all_list, columns=all_feature_names)
X_all_df['logS'] = df['logS']

y = X_all_df['logS'].values
X_all_df = X_all_df.drop('logS', axis=1)

# 選択する特徴量のリスト
features_strategy_VIF = [
    "MolLogP", "NumRotatableBonds", "AromaticProportion",
    "NumHDonors", "NumHAcceptors", "NumRings", "NumHeteroatoms"
]
X_strategy1_df = X_all_df[features_strategy_VIF]

X_train, X_test, y_train, y_test = train_test_split(X_strategy1_df, y, test_size=0.2, random_state=42)
model_VIF = LinearRegression().fit(X_train, y_train)
y_pred_VIF = model_VIF.predict(X_test)
rmse_VIF = np.sqrt(mean_squared_error(y_test, y_pred_VIF))
r2_VIF = r2_score(y_test, y_pred_VIF)

print(f"選択した特徴量: {features_strategy_VIF}")
print(f"RMSE: {rmse_VIF:.4f}")
print(f"R² (決定係数): {r2_VIF:.4f}")
# 出力
選択した特徴量: ['MolLogP', 'NumRotatableBonds', 'AromaticProportion', 'NumHDonors', 'NumHAcceptors', 'NumRings', 'NumHeteroatoms']
RMSE: 1.0741
R² (決定係数): 0.7559

R² (決定係数): 0.7559 とVIFによって選択した7個の特徴量で今までで一番良い精度が出ました。

不要な特徴量を削除したにもかかわらず、モデルの予測能力は落ちていません。これは、削除したMolWtやTPSAが持っていた情報が、残りの特徴量で十分にカバーできていることを意味します。

それぞれの特徴量の係数も見てみましょう。

print("\n--- 特徴量の係数 ---")
for name, coef in zip(features_strategy_VIF, model_VIF.coef_):
    print(f"{name}: {coef:+.3f}")
# 出力
--- 特徴量の係数 ---
MolLogP: -0.776
NumRotatableBonds: -0.132
AromaticProportion: -0.098
NumHDonors: -0.155
NumHAcceptors: +0.212
NumRings: -0.425
NumHeteroatoms: -0.175

MolLogP、NumRingsが最も効いていますね。線形回帰だとこうして係数の重みが見れるので、解釈性が高いのが良い点ですね。

NumHDonorsの係数がマイナスになっています。これも本来ならプラスに効きそうですが、NumHAcceptorsなど他の特徴量との複雑なバランスの中で、モデルがこのような重み付けに調整した結果とも考えられます。多重共線性の大きな問題は解消されましたが、特徴量間の微妙な相互作用は依然として存在しており、これもまたモデルの面白い側面です。

まとめ

これらの係数を総合的に見ると、最終的なモデルが学習した溶解度の予測は、以下のように要約できます。

「油っぽくなく（MolLogPが低く）、環状構造が少なく（NumRingsが少なく）、水分子と水素結合できる部位（NumHAcceptors）が多い分子ほど、水によく溶ける」

これは、化学者の視点からも、理にかなった結論だと思います。
特徴量選択を経ることで解釈性の高いモデルを手にすることができました。

次回はランダムフォレストやフィンガープリントを扱っていきたいと思います。

以上です。最後まで読んでいただきありがとうございました！

著者プロフィール
この記事を書いた人
RIO

大学で有機化学を専攻していた人 / 修士→博士→化学メーカー研究職 / 大学院での経験、研究職の仕事、勉強記事など発信していきます！ / 学部時代は企業でプログラミング業務のインターンシップをしてました。
Xやnoteで就活系の発信もしてます！

RIOをフォローする
プログラミング化学で機械学習
スポンサーリンク
シェアする
RIOをフォローする
RIO
スポンサーリンク

コメント

タイトルとURLをコピーしました