点群を理解するために
今回は点群を学んだので備忘録としてまとめてみようと思います。
無機化学の授業で出てくる点群、結構わからない人多いのではないでしょうか。
僕も授業でやったときはわからなかったです。わからないままにするのもなんかなぁと思ったので勉強し直してみました。
点群を学ぶことで、錯体や分子振動などの理解が深まるはずです!
ちなみに私は以下の本で点群を勉強しました。
対称操作とは?
対称操作とは分子を動かす前と同じように見えるように動かすことです。
H2Oを例に見てみましょう。
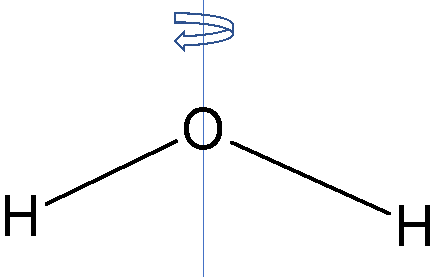
H2Oは図の青い軸に沿って180°回転しても見た目は同じですね。O原子に串をぶっ刺して180°回転させると考えてください。
このように見た目が同じになるように動かすことを対称操作と言います。
対称操作には今の例の回転の他に反転や鏡映、回映などが存在します。この記事ではこれらの対称操作と対称操作により導くことができる点群を理解していきます。
対称要素とは
対称要素とは固定する点、線、面のことでこれらの最低1つに対して回転などの対称操作を行います。
つまり、対称要素が回転や反転をするために固定する直線や面、点であって、対称操作は実際に回転や反転などをすることです。
いまいちピンとこない方も以下の説明で具体例を挙げていきますので、とりあえず読み進めてみてください。
対称操作と対称要素の関係はこんな感じです。
| 対称操作(記号) | 対称要素 |
|---|---|
| 恒等操作(E) | 全ての空間 |
| n回回転(Cn) | n回回転軸 |
| 鏡映(σ) | 鏡面 |
| 反転操作(i) | 反転中心 |
| 回映(Sn) | n回回映軸 |
対称操作の記号は斜体で記述するそうです。もちろんこの段階でこの表の意味はわからなくても大丈夫です。
では具体例と共に対称操作を説明していきます。
対称操作
恒等操作 E
恒等操作はどんな分子にもある対称操作です。とりあえず全ての分子で恒等操作はあると考えてください。
n回回転 Cn
n回回転とは対称要素のn回回転軸という直線を360°/nだけ回転する対称操作です。最初の水のように180°回転する場合、回転させる直線(回転軸)を180°(360°/2)回転させるのでC2と表せます。
つまり、回転軸を120°回転させる場合はC3、90°回転させる場合はC4となりますね。
主軸とは
対称操作を理解するために重要な主軸について説明します。
主軸とはn回回転軸の中でもnが最も大きく、より多くの原子を通る軸です。
BH3の主軸はどうなるでしょう?
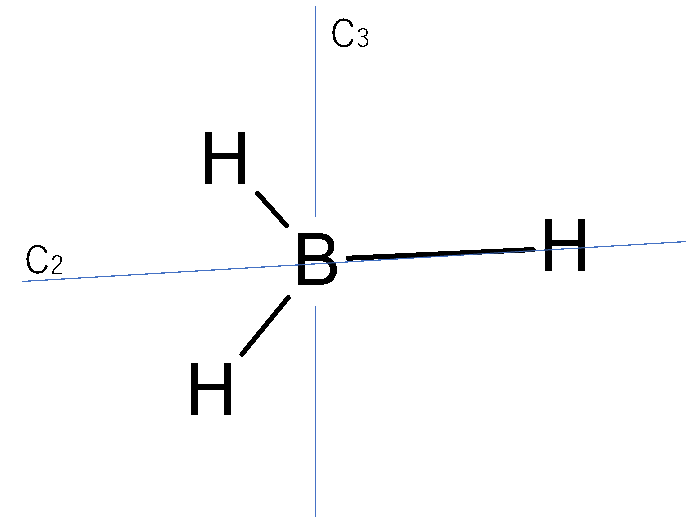
BH3は平面構造なのでH-B-Hの結合角は120°ですね。よってC3軸とC2軸があります。
nが大きい方が主軸となるのでBH3の主軸はC3ですね!
C10H20の場合はどうでしょう?
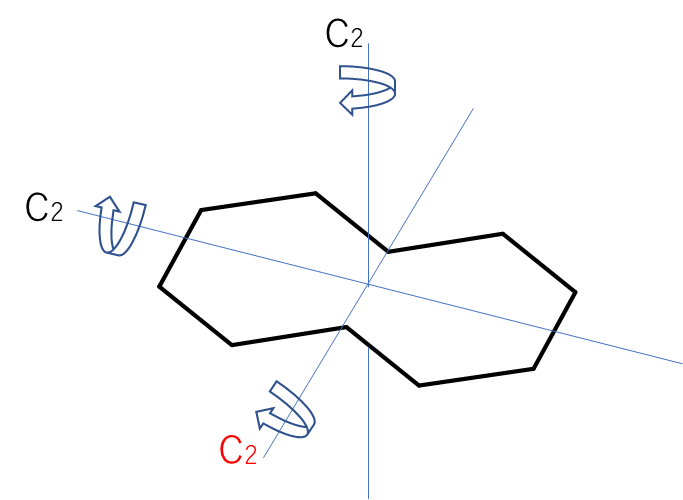
C2軸が3つありますね。最も多くの原子を通るのが主軸なのでこの場合、赤で示したC2が主軸です。
以上が主軸とn回回転軸についてです。
鏡映 σ
鏡映σは鏡で分子を真っ二つにします。イメージはこんな感じです。
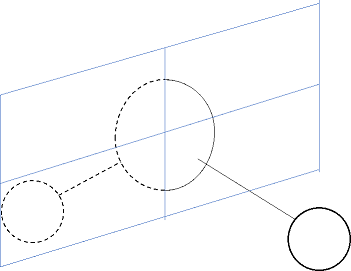
ちょっとわかりづらいかもしれませんが、青い壁が鏡と考えてください。
正面から見るとこんな感じです。
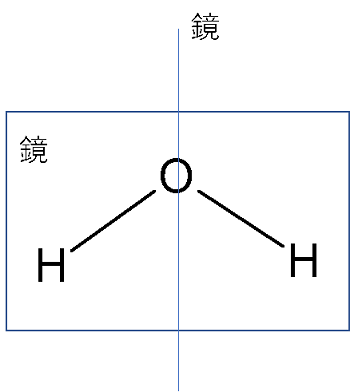
鏡でH2OのH-O-Hのなす角を2等分しています。このときH2Oの半分が鏡に映ります。これは元の状態のH2Oとまったく同じものですね。
よって水分子は鏡映面を持つと言えます。
σv
鏡映面が分子の主軸を含んでいるときの対称操作がσvです。
vはvertical(垂直)のことらしいですが、次で紹介するσhと混乱してしまうので僕は鏡映面が分子の主軸を含むと覚えています。
先ほどの水もσvがあります。
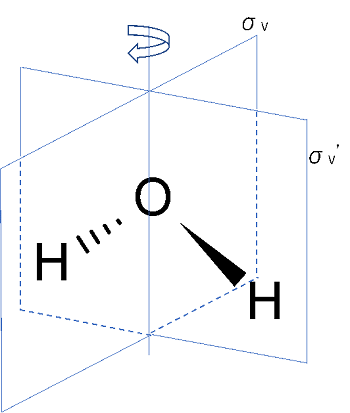
H2Oのすべての原子を含む面がσv‘、σの例で挙げたH-O-Hのなす角を2等分するのがσvです。
σvは必ず主軸を含む面でないといけません。
σh
σhは主軸に垂直な面です。hはhorizontal(水平)という意味だそうです。
主軸の説明のときに紹介したBH3で考えてみましょう。
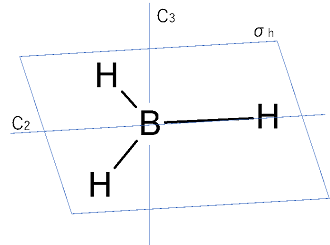
これも図が少しわかりにくいかもしれませんが、σhはBH3のすべての原子を含む面です。
つまり、主軸C3はσhとなす角が90°で垂直ですね。このような鏡面に映しても元と同じものなのでBH3はσhがあると言えます。
σd
個人的には一番わかりにくいのがσdだと思います。σvとσdの違いって難しいですよね。
σdのdはdihedral(2面角)を意味します。
なぜ2面角なのかというと、2面角を二等分する鏡映面がσdだからです。
XeF4の例を見てみます。すべての対称要素を示すと図がわかりにくくなるのでσhとC2から見てみます。
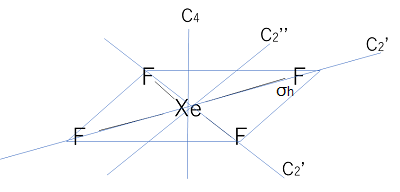
主軸はC4ですね。主軸と垂直なσhもすぐ見つけることができます。
C4と直交するC2‘とC2“がありますね。C2“は右側からも記述できるので、C2‘、C2“は2つずつありますね。
σvも見てみましょう。
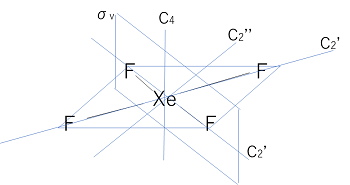
C2‘はF-Xe-F上を通っています。この二つのC2‘がなす角が二面角とするとσdはそれを二等分しています。σvはC2‘とC4を通る鏡面です。σdはC2“とC4を通る鏡面です。
2つのσvを書いて考えると二面角のイメージがしやすいかもしれません。
ここXeF4のσvとσdの違いはやはり二面角を二等分するかしないかです。
さらに詳しいσdの条件は、「主軸に直交する他の回転軸」が作る二面角を二等分し、自身も主軸を含む鏡面のことです。
修飾語が多いので「」を付けました。
少しややこしいので、σdの見分けは問題などを解いて慣れるのがいいと思います。
反転操作 i
この操作では反転中心を見つけます。反転中心とは分子の中心が原点としたとき、(x,y,z)の位置にある原子を中心を通り(-x,-y,-z)に移動させ、もともと(-x,-y,-z)にあった原子を(x,y,z)の位置に移動させたときに、元の分子と同じになる点です。
具体的に見てみましょう。
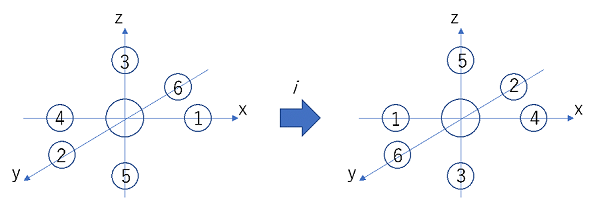
原点の原子(点)に対してこのような操作をしても元の分子と同じものであれば反転中心を持つと言えます。
ちなみに下のような、ねじれ形配座のエタンもiを対称操作として持つと言えます。
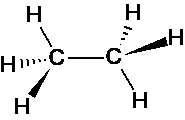
炭素原子の間を中心としてHを対角方向に同じ距離だけ移動させると、元と同じであることがわかりますね。
回映 Sn
これも個人的にややこしいと思います。
対称要素はn回回映軸のため軸を考えます。
ざっくり言うと、Snはn回回映軸を360°/nだけ回転して、その軸と垂直に交わる鏡に映したとき元の分子と同じかで判断します。
トランス-1,2-ジクロロエチレンを例に見てみましょう。

まず、C2の操作を行い、その後、C2軸と垂直な鏡面に対し鏡映操作を行います。この操作をしても元と同じになるイメージです。このとき2回回映軸でS2です。すなわち、上の図だとC2がS2となります。
また、鏡映がわかりにくいときは有機化学でキラルか判断したときのように鏡に映すことをしても同じ結果になるのでおすすめです。下の図が例です。
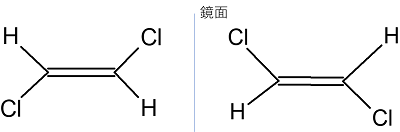
次にねじれ形配座のエタンの例を見てみましょう。ねじれ形配座のエタンはS6を対称操作として持ちます。
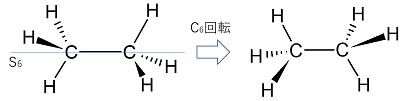
まず、S6軸なので60°回転させますね。次に鏡映操作で元と同じかを判断します。

同じ分子になっていますね。鏡映がわかりにくい場合は鏡に映してみましょう。
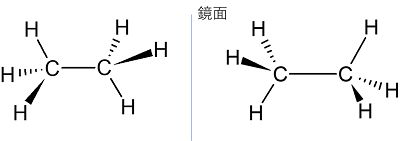
回映も複雑になると難しいので問題を解くなど練習が必要です。
対称操作からわかること
補足をしておくと、別の対称操作でも「やってることは同じ」という例がいくつかあります。
例えば、S2とiが同じということです。これはトランス-1,2-ジクロロエチレンの例ですね。このときはS2よりiを優先して記述します。
また、σhとS1が同じです。このときはσhを優先して対称要素とします。
これで一通りの説明は終わりです。
点群を帰属するには、無機化学などの教科書によく載っている「点群を帰属するための枝分かれ図」があるのでそちらを参考にしてみてください。
対称操作を正しく決定できればあとは枝分かれ図に沿って点群を決定するだけです。
この後は指標表やSALCについても勉強したいと思うので、興味のある方は見ていただけると幸いです。
無機化学の記事は他にも下のようなことを書いています。
以上です。最後まで読んでいただきありがとうございました!




コメント