射影演算子は、群論を用いてSymmetry Adapted Linear Combination (SALC) を構築する際の中心的なツールの一つです。射影演算子は、ある特定の対称性種に属する関数を抽出するために使用されます。
以下に、射影演算子とその使用方法を示します。
射影演算子の定義
射影演算子 PRの定義は以下のとおりです。
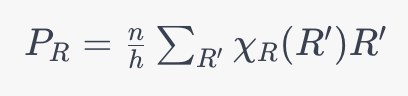
ここで、
- Rは既約表現を指します。
- nは既約表現Rの次元です。
- hは点群の順序(操作の数)です。
- R‘は点群の各操作を指します。
- χR(R‘)は既約表現Rの指標です。
SALCの構築
射影演算子を用いて、基底関数セットφからSALC φRを構築する方法は次のとおりです。
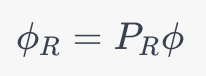
この式を用いて、既約表現Rに属するSALCを取得できます。
使用例
ナフタレンの10個のp軌道を考え、ある特定の対称性種Rに対応するSALCを構築したい場合、射影演算子を以下のように使用します。
- ナフタレンのp軌道に関する変換行列を取得します。
- 上述の射影演算子の定義を用いて、対称性種Rの射影演算子PRを計算します。
- 各p軌道に射影演算子を作用させ、SALCを取得します。
これにより、特定の対称種Rに属するSALCが構築できます。射影演算子は、このようにして分子の各軌道や振動の対称性を考える際に使用します。


コメント