大学院の授業で点群、指標表、SALCあたりの話があったので、備忘録も兼ねて少しまとめようと思います。化学系の学生に向けて、指標表の使い方、SALCの求め方の流れが伝えられればと思いこの記事を書きました。この分野は数学的な話も出てきて難しく感じますが、実際に手を動かして学べるようなるべく端折らずに書いたので、よかったらSALCを求める経験をしてみてください。
ちなみに私は以下の本でSALCや点群を勉強しました。
SALCとは
SALCは対称適合線形結合(symmetry adapted linear combination)の略です。これだけでは何のことかわかりませんね。SALCとは、分子の軌道の対称性に基づいて軌道を線形結合し、分子軌道を表現する手法です。これにより、複雑な分子軌道をよりシンプルな対称性の高い軌道の組み合わせで表現し、化学的な性質や反応の理解へと役立てます。現段階でわからなければ、点群などで学んだ分子の対称性を用いて、SALCという分子軌道の組を作ることで、軌道のエネルギー準位や分光学に役立てる、といった認識をしておけば良いかと思います。SALCを求めることがこの記事の目的なので、最初はイメージできなくて大丈夫です。臆さず進みましょう。
ナフタレンのSALCを求める準備
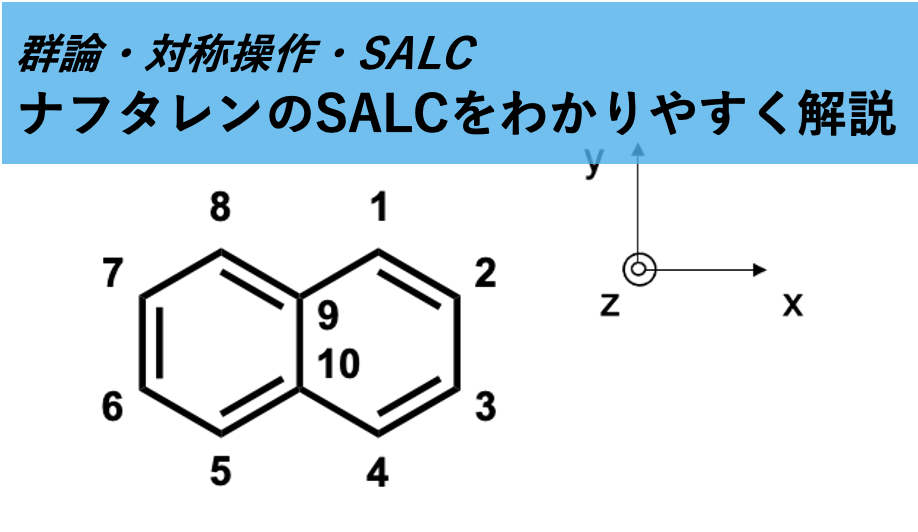
今回は以下のようにラベル付されたナフタレンの10個のp軌道から、規格直交な10個のSALCを構築してみます。

初めてSALCについて勉強するという人はまずは流れを押さえてみてください。ナフタレン以外にも何個か記事を書く予定です。
SALCを求める流れ
手順は以下の通りです。
- 点群と指標表の把握
- 対称操作による軌道の移動を考え可約表現を求める
- 可約表現を既約表現に簡約する
- SALCを構築する
次のセクションからこの手順を1つ1つ解説します。
点群と指標表の把握
SALCを求める際は分子の点群とその点群の指標表を用います。
【指標表とは】 化学においても、分子対称性の理解や分子振動の解析などで群論が用いられます。指標表は、これらの状態がどのように変換するかを整理した表として使用されることがあります。具体的には、分子が属する点群に基づいて、各対称操作(回転、反転など)が分子の電子状態や振動状態にどのような影響を与えるか、を表すために指標表が用いられます。
今回はSALCを求める手順に集中したいので、ひとまずこの2つはすでに判明しているとしましょう。本記事を通して、指標表の使い方がなんとなくわかるかと思います。
ナフタレンの点群はD2hに分類されます。D2hの指標表を以下に示します。
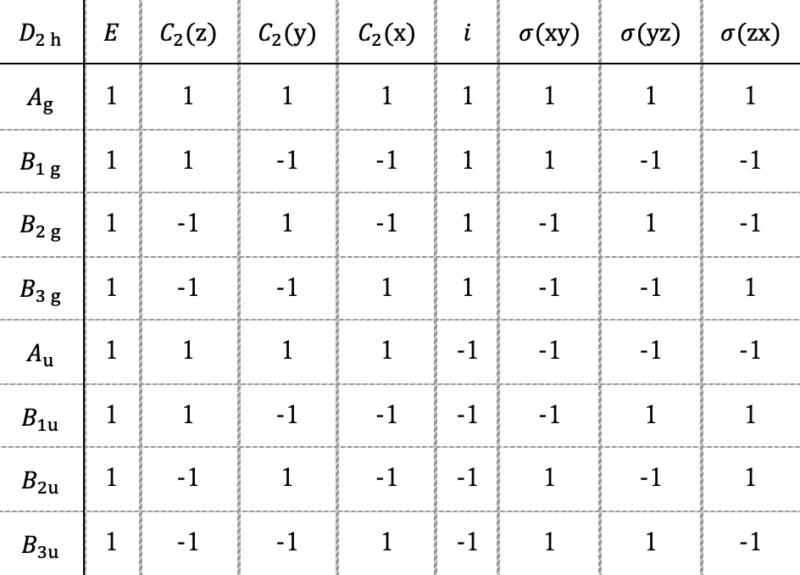
対称操作による軌道の移動を考え可約表現を求める
D2hの指標表に示された対称操作によって、最初に番号づけをした10個のp軌道がどのように移動するかを考えます。
D2hには{E, C2(x),C2(y), C2(z), i, σ(xy), σ(yz), σ(zx)}の8個の対称操作があるということが指標表の一番上の行からわかります。左列のAg, B1gなどはまだ使わないので、一旦気にしなくて大丈夫です。
対称操作による軌道の移動とは何かを説明します。例えば、p1にz軸周りの2回回転C2(z)を作用させると、p5へ移動します。
もう一つ例を挙げると、p1は反転操作iによって-p5へ移動します。-がつくのは反転操作でp軌道の位相が反転するためです。
他の対称操作やp軌道についても考えると、以下の表が書けます。これは、一番左の列に書かれたp軌道が一番上の行の対称操作によって、どこへ移動されるかをまとめた図です。
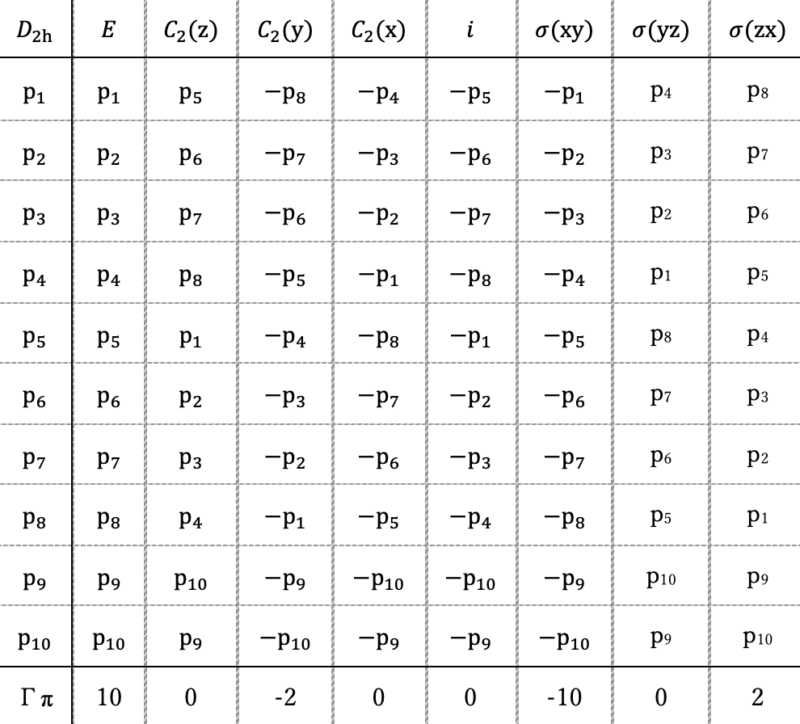
先ほどの表の一番下の行にΓπという記号があります。Γπは10個のp軌道を基底としたときの可約表現と呼ばれます。この可約表現では、軌道が異なる位置に移動すれば 0、軌道がそのままであれば+1、軌道が反転すれば-1として、全ての行での値の総和が可約表現Γπの行に入ります。
【可約表現とは 】 可約表現とは、群論において、与えられた群の表現がさらに小さな表現に分解できる場合にその表現のことを指します。ここでのケースで言うと、Γπは10個のp軌道の移動を考えて得られたものであるため、例えば10個の内4個のp軌道は同じ対称性で議論できる、といった感じです。
この可約表現Γπは簡約化という操作を行うことができます。簡単に言うと、D2hの対称種Ag、B1g…などの和(直和と呼ばれる)でΓπを表すということです。可約表現をより小さな対称性を持ったグループに分解するといったところです。例えば基底(10個のp軌道)のうち、p1とp2だけで表現できる操作をまとめてしまい、計算量を少なくできます。
わからない言葉ばかりで難しければ、とりあえず先に進んで、式と表の関係を見ながら手を動かしてみましょう!
可約表現を既約表現に簡約する
ナフタレン10個のp軌道を基底とした時の可約表現ΓπをD2hの指標表の既約表現に簡約します。可約表現Γπは指標表のi番目の既約表現(指標表のAgやB1gなど)の和(直和と呼ばれる)で表されます。
簡約化では、この和の各項の係数、つまりi番目の既約表現が可約表現に何回含まれるか、を求めます。これによって、10個のp軌道の移動についての情報を持つ可約表現がどの既約表現で表されるかを決定します。今、ナフタレン自身ではなくナフタレンの10個のp軌道を考えているので、これらの基底に関する対称性を議論しようとしているということですね。
簡約の式は以下のようになります。難しそうな式ですが、順を追って理解すれば中学生までの知識で計算できます。
\[ a_i = \frac{1}{h} \sum_R \chi(R) \times \chi_i(R) \]
ここで、それぞれの意味は以下の通りです。
・aiは既約表現iの出現回数
・hは点群の操作の数
・Rは点群の各操作
・χ(R)は可約表現の指標
・χi(R) は既約表現iの指標
この式を全ての既約表現に対して適用します。Agについて、例を示しながらやっていきましょう。
指標表からAgの部分を取り出すと以下のようになりますね。
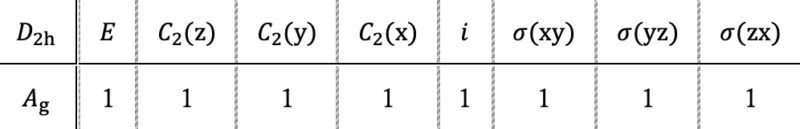
したがって、「aiは既約表現iの出現回数」でしたので、aAgを考えると、上の式のχi(R)はχAg(R)となり、Rには各対称操作が入ります。
例えば、χAg(E)=1, χAg(C2(z))=1ですね。
また、χ(R)は可約表現Γπの指標でした。
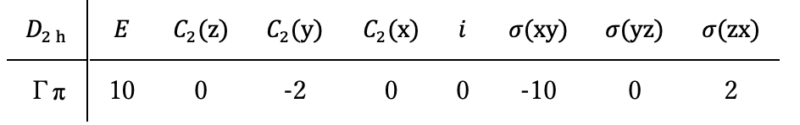
したがって、χ(E)=10、χ(C2(z))=0…となります。
つまり、aiの式のΣの中は、χ(E)* χAg(E)+ χ(C2(z))* χAg(C2(z))…となります。
計算すると、以下のようになります。
Agの係数は:
\[ a_g = \frac{1}{8} \left[ (10 \cdot 1) + (0 \cdot 1) + (-2 \cdot 1) + (0 \cdot 1) + (0 \cdot 1) – (10 \cdot 1) + (0 \cdot 1) + (2 \cdot 1) \right] \ = 0 \]
となり、0ですね。つまり、簡約化してもAgは含まれません。
Ag以外の他の表現でも同じ計算を行います。ここではスペース節約のため0にならないものだけ示します。また、[]の中身で0になる項は省略して書きます。余裕があれば実際に0になるものも計算して確認してみてください。
\[ a_{B2g} = \frac{1}{8} \{1 \times 1 \times 10 + 1 \times 1 \times (-2) + 1 \times (-1) \times (-10) + 1 \times (-1) \times 2\} = 2 \]
\[ a_{B3g} = \frac{1}{8} \{1 \times 1 \times 10 + 1 \times (-1) \times (-2) + 1 \times (-1) \times (-10) + 1 \times 1 \times 2\} = 3 \\ \]
\[ a_{Au} = \frac{1}{8} \{1 \times 1 \times 10 + 1 \times 1 \times (-2) + 1 \times (-1) \times (-10) + 1 \times (-1) \times 2\} = 2 \\ \]
\[ a_{B1u} = \frac{1}{8} \{1 \times 1 \times 10 + 1 \times (-1) \times (-2) + 1 \times (-1) \times (-10) + 1 \times 1 \times 2\} = 3 \\ \]
したがって、先ほどの可約表現Γπは簡約でき、
\[ \Gamma_{\pi} = 2B_{2g} + 3B_{3g} + 2A_{u} + 3B_{1u} \]
と計算できます。これは、ナフタレンの10個のp軌道に基づく分子軌道が、これらの4つの対称種の組み合わせで表現できるということを意味します。
この操作が簡約化と呼ばれます。簡約化ができたら、次で説明する操作を経てSALCが構築できます。
SALCを構築する
SALCを構築する操作は射影演算子という、「ある特定の対称性種に属する関数を抽出する操作」に基づいています。射影演算子の式は以下のようにかけます。
\[ \widehat{P}_\Gamma = \frac{n}{h} \sum_{R} \chi_\Gamma (R) \widehat{R} \]
- n は既約表現の次元(B2gの場合は1)
- h は点群の対称操作の総数(D2hの場合は8)
- χτは既約表現の指標

p1軌道にこの射影演算子を作用させると:
\[ \widehat{P}_{B2g}(\hat{p}_1) = \frac{1}{8} \left[ \chi_{B2g}(E) \cdot p_1 + \chi_{B2g}(C_2(z)) \cdot p_5 + \chi_{B2g}(C_2(y)) \cdot (-p_8) + \chi_{B2g}(C_2(x)) \cdot (-p_4) + \chi_{B2g}(i) \cdot (-p_5) + \chi_{B2g}(\sigma(xy)) \cdot (-p_1) + \chi_{B2g}(\sigma(yz)) \cdot p_4 + \chi_{B2g}(\sigma(zx)) \cdot p_8 \right] \]
第一項は対応する対称操作をp1に作用させた後の形です。
つまり、第二項
\[ \chi_{B2g}(C_2(z)) \cdot p_5 \]
のp5はもともとC2(z)をp1に作用させたものです。したがって、
\[ \hat{P}_{B2g}(\hat{p}_1) = \frac{1}{8} \left[ (1)(p_1) + (-1)(p_5) + (1)(-p_8) + (-1)(-p_4) + (1)(-p_5) + (-1)(-p_1) + (1)(p_4) + (1)(p_8) \right] \]
\[ = \frac{1}{8} \left[ 2p_1 – 2p_5 + 2p_4 – 2p_8 \right] \]
\[ = \frac{1}{4} \left[ p_1 – p_5 + p_4 – p_8 \right] \]
この射影演算子の操作に従い、B2gのSALCは、B2gの射影演算子がそれぞれのp軌道(p1からp10)に作用した結果を全て足し合わせたものになります。しかし、ここで注意が必要です。
SALCを構築する際には、p軌道の特定の部分集合ごとに射影演算子を作用させることで、独立したSALCを得ることができます。今回の場合は、(p1,p4,p5,p8)、(p2,p3,p6,p7)、(p9,p10)が等価なp軌道であり、部分集合とみなせます。
つまり、射影演算子が作用した結果を全て足し合わせる際は、この部分集合ごとに行う必要があります。以下、具体例を示します。
\[ 1: \hat{P}_{B2g}(\hat{p}_1) = \frac{1}{4} [p_1 – p_5 + p_4 – p_8] \\ \]
\[ 2: \hat{P}_{B2g}(\hat{p}_2) = \frac{1}{4} [p_2 – p_6 + p_3 – p_7] \\ \]
\[ 3: \hat{P}_{B2g}(\hat{p}_3) = \frac{1}{4} [p_3 – p_7 + p_2 – p_6] \\ \]
\[ 4: \hat{P}_{B2g}(\hat{p}_4) = \frac{1}{4} [p_4 – p_8 + p_1 – p_5] \\ \]
\[ 5: \hat{P}_{B2g}(\hat{p}_5) = \frac{1}{4} [p_5 – p_1 + p_8 – p_4] \\ \]
\[ 6: \hat{P}_{B2g}(\hat{p}_6) = \frac{1}{4} [p_6 – p_2 + p_7 – p_3] \\ \]
\[ 7: \hat{P}_{B2g}(\hat{p}_7) = \frac{1}{4} [p_7 – p_3 + p_6 – p_2] \\ \]
\[ 8: \hat{P}_{B2g}(\hat{p}_8) = \frac{1}{4} [p_8 – p_4 + p_5 – p_1] \\ \]
\[ 9: \hat{P}_{B2g}(\hat{p}_9) = 0 \\ \]
\[ 10: \hat{P}_{B2g}(\hat{p}_{10}) = 0 \]
1,4,5,8は(p1,p4,p5,p8)の項のみを含み、2,3,6,7,は(p2,p3,p6,p7)を含むといったように集合ごとに結果がまとまっていますね。
B2gのSALCは、B2gの射影演算子がp軌道に作用した結果をこれらの集合ごとに全て足し合わせたものになるため、この結果から、以下の2つのB2gの対称性を持つSALCが得られます。
\[ B2g: \frac{1}{2} (p_1 + p_4 – p_5 – p_8) \\ \]
\[ B2g: \frac{1}{2} (p_2 + p_3 – p_6 – p_7) \\ \]
可約表現Γπは、
\[ \Gamma = 2B_{2g} + 3B_{3g} + 2A_{u} + 3B_{1u} \]
と簡約できていました。B2gの係数が2であったことはB2gの対称性を持つSALCが2つあるということにもつながっています。
また、この結果から、p9とp10はB2gに寄与しないことがわかります。
同様の操作をB3g、Au、B1uでも行います。計算は省略しますが、射影演算子の操作を理解すれば容易に求まりますね。
全て書き出すと以下のようになります。
\[ B2g: \frac{1}{2} (p_1 + p_4 – p_5 – p_8) \]
\[ B3g: \frac{1}{2} (p_1 – p_4 – p_5 + p_8) \]
\[ Au: \frac{1}{2} (p_1 – p_4 + p_5 – p_8) \]
\[ B1u: \frac{1}{2} (p_1 + p_4 + p_5 + p_8) \]
\[ B2g: \frac{1}{2} (p_2 + p_3 – p_6 – p_7) \]
\[ B3g: \frac{1}{2} (p_2 – p_3 – p_6 + p_7) \]
\[ Au: \frac{1}{2} (p_2 – p_3 + p_6 – p_7) \]
\[ B1u: \frac{1}{2} (p_2 + p_3 + p_6 + p_7) \]
\[ B3g: \frac{1}{\sqrt{2}} (p_9 – p_{10}) \]
\[ B1u: \frac{1}{\sqrt{2}} (p_9 + p_{10}) \]
SALCの構築は一見複雑ですが、慣れればそこまで難しくないですし、分子軌道への理解も深まります。
おわりに
このサイトではナフタレンの他にもいくつか計算例を解説する予定ですので、チェックしてみてください。また、本格的に学びたい方は以下の書籍が有名です。
Noteで化学系就活のことや、研究生活のことなど書いているので覗いてもらえるとうれしいです!

その他おすすめ参考書↓






コメント