【初心者向けNMR講座①】αスピン、βスピン、ゼーマン分裂と共鳴周波数の関係

分子の構造を原子レベルで解き明かす強力な分析手法ですが、その原理は少し複雑に感じるかもしれません。この記事では、NMRの最も基本的な部分である「なぜ外部磁場をかけるのか？」という疑問から出発し、原子核の持つ「スピン」という性質、外部磁場下で起こる「ゼーマン分裂」、そして「共鳴周波数」というNMR測定の重要な概念を解説します。

NMRで磁場をかけるのはなぜか？αスピンとβスピン

NMRでは原子核の状態を調べます。原子核は自転しており、陽子と中性子から構成されています。
陽子と中性子のいずれかの数が奇数の原子核は核スピンという磁場に応答して向きが変化する性質を持っているため、小さな磁石と見なすことができます。

そのため、¹H NMRにおけるプロトン（¹H：スピン量子数 I = 1/2）は普段はランダムな方向を向いていますが、外部磁場（B₀）に置かれると、磁石のN極、S極のように向きが揃います。

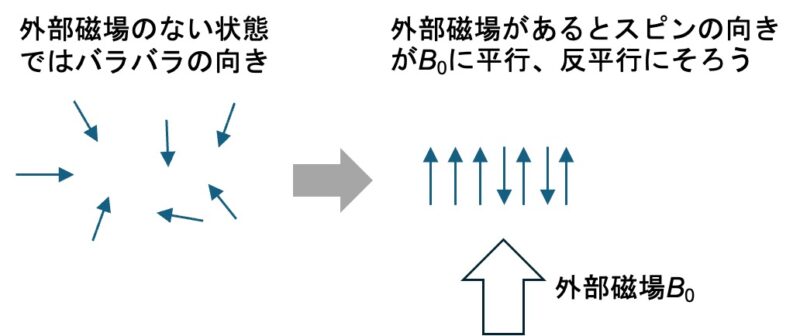
しかし、核スピンは磁石とは違い、外部磁場に平行な基底状態と反平行な励起状態という２つのエネルギー状態（スピン状態）に分裂します。これはゼーマン分裂と呼ばれる現象です。

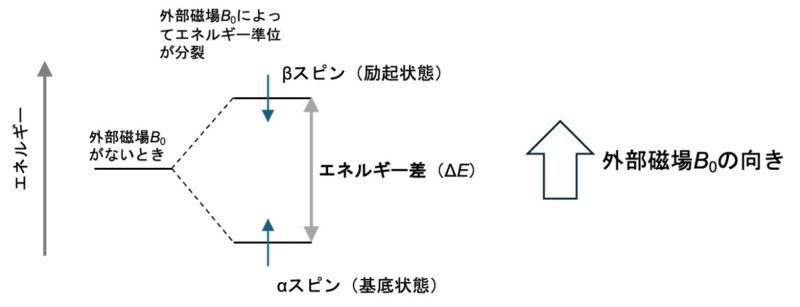
スピン状態は以下の２つです：

1. αスピン状態（低エネルギー状態, 基底状態）：外部磁場と平行
2. βスピン状態（高エネルギー状態, 励起状態）：外部磁場と反平行

ちなみに、核スピン量子数（I）によって外部磁場中で取りうる状態の数が決まります。

核スピン量子数（I）の原子核が外部磁場中で取りうる状態の数＝2I +1

共鳴周波数とエネルギー差

プロトン（¹H）が外部磁場に置かれ、エネルギー準位が分裂すると、安定なαスピン（基底状態）は電磁波に応答することができます。
つまり、αスピンは、”αスピン状態とβスピン状態のエネルギー差（ΔE）”に対応する電磁波（エネルギー）を吸収し、βスピン状態へと励起することができます。

αスピン状態とβスピン状態のエネルギー差（ΔE）は以下の式で表されます。

\[{\Delta E} = h \nu\]

ここでνは共鳴周波数と呼ばれます。
つまり、「その周波数 ν を持つ電磁波の光子1個のエネルギー (hν) が、ちょうどスピン状態間のエネルギー差 (ΔE) に等しく、核スピンの遷移（α→β）を引き起こすことができる」 ということを意味します。

実際の測定と緩和

実際の測定では、この共鳴周波数を持つ電磁波を外部磁場中で試料に照射し、核スピンの遷移を引き起こします。その後、遷移してβスピン状態になった核スピンはやがて安定なαスピン状態に戻り、その際にエネルギーを放出します。この元の熱平衡状態に戻る過程は緩和と呼ばれ、この緩和を検知して解析することでNMRスペクトルが得られます。

外部磁場との共鳴周波数の関係

共鳴周波数、そしてそれに対応するエネルギー差 ΔE は、原子核の「磁石」としての性質、そしてNMR装置が作る強力な「磁場」と関係しています。

原子核は小さな磁石： 多くの原子核は、それ自体が非常に小さな磁石のような性質を持っています。この「核の磁石」としての強さを表すのが「核磁気モーメント μ」です。

この「核の磁石としての性質（核磁気モーメント μ）」は以下の式で表されます。
\[\mu = \frac{h\gamma}{2\pi}I\]
μ：核磁気モーメント. 核の磁石としての強さのようなもの.
h：プランク定数.
γ（ガンマ）：磁気回転比. 原子核の種類ごとに決まっている定数で、原子核がどれだけ磁場に敏感に反応するかを示す. したがって、γの大きな原子核ほど磁石としての性質が強くなる.
I：核スピン量子数. 原子核が持つ固有の「スピン（自転のようなもの）」の大きさを表す.

核磁気モーメントμの原子核が、外部磁場 B₀ 中に置かれたときのエネルギー準位は、μB₀と表されます。プロトン（¹H）の場合、外部磁場 B₀ 中でエネルギー準位は
αスピン：-μB₀
βスピン：+μB₀
に分裂します。したがって、エネルギー差は以下のようになります。

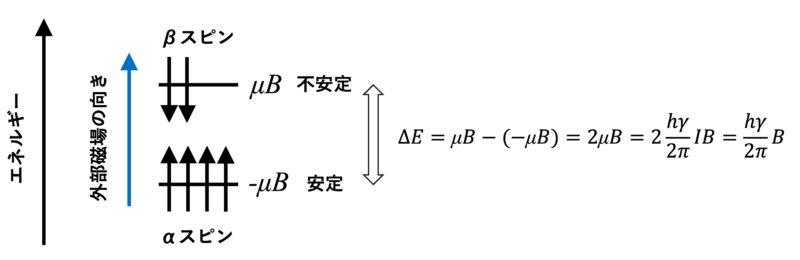
\[\Delta E = h \nu = 2\mu B_0 = \frac{h\gamma}{\pi}B_0\]

この式から共鳴周波数は
\[\nu = \frac{\gamma}{2\pi}B_0\]
と求まります。

ボルツマン分布による状態の占有率

実際にαスピン状態とβスピン状態のエネルギー差を化学的に馴染みのある kJ/mol 単位で求めてみましょう。
400 MHz NMRの場合、ν=400 (MHz) =400×10⁶ (Hz) =4.00×10⁸ (s⁻¹) となります。

\[\Delta E = h\nu\]
\[\Delta E = (6.626 \times 10^{ -34} \text{ J}\cdot\text{s}) \times (4.00 \times 10^{ 8} \text{ s}^{-1})\]
\[\Delta E = 2.6504 \times 10^{-25} \text{ J}\]
次に、このエネルギーを原子核1モルあたりに換算します。アボガドロ定数 (6.022×10²³ mol⁻¹)を用いて、
\[\Delta E = (2.6504 \times 10^{-25} \text{ J}) \times (6.022 \times 10^{23} \text{ mol}^{-1})\]
\[\Delta E = 0.159603808 \text{ J/mol}\]
\[\Delta E \approx 0.000160 \text{ kJ/mol}\]

この計算結果からもわかるように、NMRで観測されるスピン状態間のエネルギー差は非常に小さいです。
そのため、外部磁場中であってもαスピン状態のプロトンの数（N_α）とβスピン状態のプロトンの数（N_β）はほぼ同じです。

プロトンのαスピン状態とβスピン状態の数の比は、ボルツマン式に従って以下のように表されます：

\[\frac{N_{\alpha}}{N_{\beta}} = \frac{e^{-\frac{E_{\alpha}}{kT}}}{e^{-\frac{E_{\beta}}{kT}}} = e^{\frac{\Delta E}{kT}}\]

Nα​：α状態のプロトン数
Nβ​：β状態のプロトン数
ΔE：エネルギー差（ゼーマン効果による分裂）
k：ボルツマン定数
T：絶対温度

この式に従うと、常温（約300 K）での典型的なNMR測定では、10万個に1個程度の割合でα状態が多く存在します。このわずかな偏りが、NMR信号の感度を決定しています。

ラモーア歳差運動とは何か

ラ―モア歳差運動とは、原子核の持つ磁気モーメント（原子核を小さな磁石と考えたときのN極S極の向きと強さ）が、外部磁場 B₀ をかけられたときに、その磁場の方向を軸として、磁気モーメントの向きがコマのように首を振る運動（歳差運動）をすることです。
外部磁場 B₀ における歳差運動の角周波数 ω₀​ は ω₀​=γB₀​ で与えられます。

磁気回転比 γ が大きい核種ほど、また外部静磁場 B₀​ が強いほど、歳差運動は速くなります。
これが原子核の種類によって共鳴周波数が異なる原因です。
たとえば、¹Hの場合、磁気回転比は2.675×10⁸ kg⁻¹•sec•Aですが、
¹³Cでは0.673×10⁸ kg⁻¹•sec•Aとおおよそ1/4になります。

αスピンとβスピンは便宜上は外部磁場に対して「平行」、「反平行」の方向を向くと説明されますが、正確には、歳差運動しながら、少し横方向にずれた駒のような歳差運動をしてる、といえます。

フーリエ変換型NMRは別の機会に解説したいと思います。

まとめ

この記事では、NMRの最も基本的な原理であるゼーマン分裂と共鳴周波数について解説しました。

• 核スピンを持つ原子核は、外部磁場（B0​）中に置かれると、磁場の向きに対して平行な**αスピン状態（低エネルギー）と反平行なβスピン状態（高エネルギー）**という2つのエネルギー状態に分裂します（ゼーマン分裂）。
• この2つの状態間のエネルギー差 (ΔE) に相当する特定の周波数の電磁波を照射すると、αスピン状態の核スピンがエネルギーを吸収し、βスピン状態へと遷移します。この周波数が共鳴周波数 です。

これらの基本原理を理解することで、なぜNMRで構造解析ができるのか、その第一歩を踏み出すことができたはずです。

最後まで読んでいただきありがとうございました！

参考までに、筆者が大学院でお世話になったNMRのおすすめの参考書です↓
ビギナーズ有機構造解析
有機スペクトル解析

NMRの関連記事も公開中！

【初心者向けNMR講座②】化学シフトの原理とは？遮蔽効果もわかりやすく解説！

NMRの「化学シフト」とは何か、その原理を初心者にもわかりやすく解説します。なぜプロトンのシグナルはズレる？遮蔽効果、ppmスケール、基準物質TMSの役割まで、NMRスペクトル読解の基礎を学びましょう。分子構造解析の第一歩に！

butioblog.com

2025.05.22